|
ABSTRACT: Mathematics can prove that reducing aerodynamical downforce increases safety. In contrast, FIA president Max Mosley says that mathematics proves that grooves in tyres increase the safety of Grand Prix racing, because (I) the energy of an impact is proportional to the grip of the tyres and (II) whatever its speed, a car spins for exactly half the radius of the curve it is when control is lost. The faster a car is going at the point it starts to spin, the faster it will be at all points during deceleration, as it always stops in the same place. Therefore, if it hits a barrier on the way, the faster the car was going when it started to spin the harder it will hit the barrier. The greater grip of the tyres, the faster the car would have been immediately before the spin. Hence, says Mosley, reduced grip equals increased safety, everything else being equal. However, his mathematical model ignores one point: When a car spins, it looses is aerodynamical downforce, and thus grip. Here we explain the mathematics and critically discuss why we feel the FIA President's interpretations are incorrect.
For safety reasons, FIA wants to prevent that cornering speed increases. There is an ongoing discussion on whether limiting the corning speed should be by cutting more and more grooves in tyres or by reducing aerodynamical downforce, e.g. by banning wings. FIA President Max Mosley has put forward several statements based on mathematics. We explain those arguments in detail and discuss the assumptions that are made in the analysis. By making a sharp distinction between aerodynamical grip and mechanical grip, we derive an equation that reveals that reducing the aerodynamical downforce in fact leads to more safety.
Basic mathematical equations
To understand Mosley's arguments, it is necessary to start with the governing mathematical equations. Consider a racing car that drives through a corner, for simplicity a circle. Let the letter V stands for the velocity of the car, let R be the radius of the circle (see Figure 1) and m symbolises the mass (weight) of the car. Old Isaac Newton showed that if an object turns in a circle, it must be subjected to a force pointing to the centre of the circle (if there was no centre force the direction of car would be a straight line). Denote the centre force Fc. This central force is given by
|
Fc = 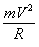
|
(1)
|
On a racing car this force is of course provided from the tyres. The side force that a tyre can deliver depends on the tyre compound and construction and on how hard it is pressed against the ground. An approximate equation for the maximum frictional force is
In equation (2) the symbol m stands for the friction coefficient between tyres and the ground and N is the normal force on the tyres; how hard they are pushed against the ground. In the mathematical language, tyres with high grip have a high value of m.
The energy that the car possess due to its velocity is called the kinetic energy, Ekin. It is
If the car slides or spins off, the driver usually locks up the tyres, such that he utilises the full friction of the tyres. The energy absorbed is the work of the frictional force. As an approximation, assume that the frictional force is constant all the time. Then the frictional work Wfric is force times distance
where the symbol d is the distance the car slides before it stops. These are the basic equations. Now we combine them.
Relationship between energy of impact and grip of the tyres
When the car drives through the corner the frictional force from the tyres are equal to the force needed, Ffric = Fc. Setting equation (1) equal to (2) gives
|
m N = 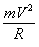
|
(5)
|
Multiplying by R on both sides gives
We note that the right hand side m V2 appears in the equation for the kinetic energy, equation (3). Thus, in equation (3) we can substitute m V2 by m N R. This gives
Recall that Ekin is the kinetic energy the car possesses when it drives through a curve. This proves Mosley's first statement; the energy of an impact is proportional to the grip of the tyre.
Distance a car slides before it stops
Imagine now that the car spins off, as shown in Figure 2. The car stops when all the kinetic energy has lost by the frictional force. Actually, energy is also lost to aerodynamical drag. This is neglected in the simple model described here. Setting the work of the frictional force of the tyres, Wfric from equation (4), equal to Ekin from equation (7) gives
By (2) we can substitute m N for Ffric. This gives
The left hand side is the energy loss during the spin, and the right hand side is the kinetic energy the car possesses before the spin. The product m
N appears on both sides, so it cancels out. The sliding distance simply becomes
This is Mosley's second statement: The car stops exactly half the radius of the curve it is on when control is lost.
|
Separating effects of mechanical and aerodynamical grip
To derive the equations above, it was assumed that the friction force from the tyres, Ffric, was the same all the time. Let us take a closer look at that assumption. How well does it fit to reality?
A car that spins off onto grass or gravel may experience a smaller friction than when it ran on the tarmac, simply because the friction between rubber and tarmac is higher than between rubber and grass. If the friction during the spin is lower, the sliding distance increases, i.e. d exceeds ½ R.
| 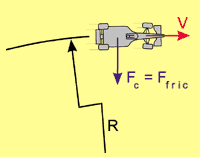
| Figure 1. A racing car that drives through a circle having a radius R at a velocity V requires a central force Fc. As long as the tyres roll, they deliver a side force Ffric (shown in blue colour). |
|
|
|
Another very important issue is aerodynamics. Before the car spins, it fully utilises the aerodynamical downforce created by the underbody and wings. The normal force on the tyres is higher than what would result for a car with no downforce. Therefore the maximum frictional force (equation (2)) will be higher.
But when the car spins, the direction of airflow will no longer reach the wings from the frontal direction. Also, the downforce that is produced by the underbody and diffuser at the rear end of the car is lost (it is well known that the underbody aerodynamics is very sensitive to the ride height). As a result, most of the aerodynamical downforce disappears during a spin. Only the gravity force contributes to the normal force on the tyres. The frictional force during breaking is thus lower than the frictional force during cornering. This can be brought into the mathematics as follows.
| 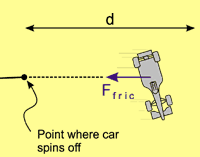
| Figure 2. The racing car spins off when the required centre force Fc exceeds the maximum side force that the tyres can provide. The car spins off a distance d before it stops. When the tyres are locked up, the frictional force from the tyres Ffric (blue colour) now acts in the opposite direction of sliding. |
|
|
Before the spin, the normal force on the tyres, N, comes from two sources, the gravity force (weight) of the car and the aerodynamical downforce. This can be written mathematically as
In this equation m again symbolises the mass of the car, g is the gravity acceleration and Faero is a symbol for the aerodynamical downforce (used in connection with equation (2), the first term in (11) is sometimes called the mechanical grip, and the second term is called aerodynamical grip).
During the spin, most of the aerodynamical downforce is lost. Therefore, it is reasonable to assume that all the vertical force on the tyres is the weight of the car
We proceed to insert equation (11) for the right side of equation (9), and (12) into the left hand side of equation (9). The result is
|
m m g d = ½ m (m g + Faero) R
|
(13)
|
The coefficient of friction m again appears on both sides and cancels out. By dividing both left and right hand sides by m m g we find the distance the car spins before it stops
|
d = ½ (1 + Faero/m g) R
|
(14)
|
The ratio between the aerodynamical downforce and the gravity force on the car, Faero/m g, can easily be in the order of 1-2 for a Formula One racing car (it varies from one bend to the next, depending on the velocity). As an example, set Faero/m g equal to unity. Inserting this into equation (14) gives
This result shows that when aerodynamical force is included the distance to stop the car is longer than if the aerodynamical force is ignored, equation (10). In fact, for this particular example the distance to stop the car, d, (equation (15)) is now twice as long as if there was no aerodynamical downforce (equation (10)). In conclusion, increasing the aerodynamical downforce increases the spinning distance, d.
Recall Mosley's argument: The faster a car is going at the point it starts to spin, the faster it will be at all points during deceleration. We can now add the following: The higher the downforce, the faster the car can drive through a curve. If it subsequently spins, the distance it slides before it stops is longer. Therefore, if the car hits a barrier on the way, it will hit the barrier harder.
Increasing tyre grip and reducing aerodynamical downforce?
Some drivers have suggested that the mechanical grip should be increased (e.g. by re-introduction of slick and thus softer tyres), while the aerodynamical grip should be decreased. In mathematical terms this is equivalent to an increase in m and a decrease in Faero. If Faero is sufficiently low, such that the product m N remains lower than before, the kinetic energy (equation (7)) may still be lower than before. Also, by equation (14) the stopping distance will be shorter when Faero/m g is smaller. The mathematics shows that the drivers are right: Reducing the aerodynamical grip and increasing the mechanical grip will increase safety.
In addition, this approach is likely to allow closer racing, since the current cars looses their aerodynamical downforce, because the airflow is disturbed when following another car closely. If most of the grip came from the mechanical grip of the tyres, this loss of grip would not appear and closer racing would be possible.
Reducing aerodynamics and using slick tyres is the direction chosen in the Champ Cars series. On super speedways a specially designed low-downforce, high drag rear wing, called "Handford Wing", is mandatory. And... does not the Champ car series have more close racing than Formula One?
List of symbols
| d | | distance the car spins before it stops |
| g | | gravity acceleration |
| m | | mass of the car |
| Ekin | | kinetic energy of car just before spin |
| Faero | | aerodynamical downforce |
| Fc | | centre force required for making the car turn |
| Ffric | | frictional force from the tyres |
| N | | normal force on tyres |
| R | | radius of curve the car drives through before spinning |
| V | | velocity of car before the spin |
| Wfric | | work of frictional force |
| m | | friction coefficient between tyres and ground |
Authors
Bent Sørensen is 37 years old and has a Master of
Science and a PhD in mechanical engineering. His specialization is solid
mechanics. On the side, Sørensen creates Formula One technical drawings.
His drawings are published in motorsports magazines worldwide. Some of his work can in the third edition of
Sal Incadela's book "The Anatomy & Development of the Formula One Racing Car from 1975" (1990).
Svend Damborg is an auto mechanic. In the 70's, he worked with Denmark's leading racing drivers and participated in numerous races, including nine Monte Carlo Rallies.
| 
